For three centuries, musicians argued passionately about how so split an octave up into twelve notes. It wasn't that nobody had heard of today's compromise solution, Equal Temperament, but it was rejected on the grounds that Equal Temperament couldn't express the subtle nuances of musical intervals which the composers of the day were exploiting.
A lot of solutions, or temperaments were proposed, some of which remain popular to this day among musicians who play historical music: particularly music from the renaissance and baroque periods. A new generation of musicians are now exploring microtonal temperaments, which deal with the same compromises. By the way, the issues which caused different temperaments to be explored, also exist in musical scale other than our western diatonic scale.
Temperament Designer lets you easily design your own temperaments.
What’s a
|
Music is based on sounds at different pitches, or frequencies. We usually make music with a relatively small set of pitches, each of which is called a note. A temperament is a way of deciding just what the pitch will be for each note. |
||||||||
A bit of theory |
We call the difference between two pitches an interval. Mathematically, the interval between two pitches is the ratio of their frequencies. For example, let’s take two pitches: the A above middle C, and the A just below middle C. The top A has a frequency of 440 Hz, and the lower A has a frequency of 220 Hz. The ratio between these two pitches is 440/220, which is mathematically equivalent to a ratio of 2/1. This interval is called an octave, and is found in almost all musical systems. |
||||||||
Pure Intervals |
In general, intervals where the frequencies are the ratio of two small numbers, sound better to our ears than intervals which aren’t. Some of the important intervals in Western music are: 1/2 = an octave |
||||||||
Incompatible Intervals |
Ideally, we would like to define a reasonably small group of pitches which would let all of these intervals be used freely. Unfortunately, this goal is unattainable. We can demonstrate this by playing a circle of fifths. Start with any note, and play the note which is exactly a major fifth above it. Keep going, doubling back an octave when you have to, until you get back to your starting note. After playing 12 major fifths, you will have played every note exactly once, and also defined every interval that exists in a diatonic scale. But ... If you followed the instructions, and played every major fifth as a pure interval, you would have ended up being about a quarter of a semitone away from your starting pitch. We can demonstrate the same thing with a bit of arithmetic. There are twelve consecutive fifths in a circle of fifths. The same interval is covered by seven consecutive octaves. Saying this in mathematical terms:
The interval between seven octaves and a circle of fifths is about 23% of a semitone, and is referred to as a Pythagorean comma. The object of a temperament is to hide this comma somewhere where it won't sound too obvious. |
||||||||
Here's what you see when you use Temperament Designer. You see three circles:
It's a lot of information in a very compact form! Once you're worked out a temperament, you can try it out, and see how it sounds to you.
|
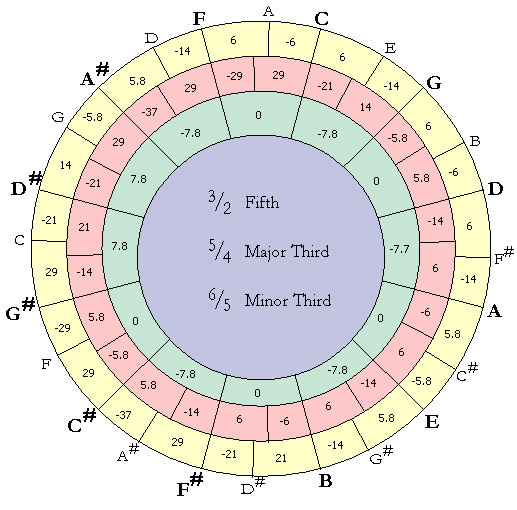 |
||||||||
|
Traditionally, temperaments have been built by modifying the major fifths. We make it easy for you by giving you sliders for each major fifth. The sliders automatically adjust to keep the overall adjustment (or comma) correct. The units you are looking at is the comma. You can specify either the Pythagorean, or the Syntonic comma (which we haven't talked about yet). The example we've been looking at is a historical temperament called Werkmeister IV. This is a temperament that give you almost pure major fifths and major thirds in key signatures with up to three sharps, or two flats. In many cases, music which these key signatures will sound startlingly clearer than if it is played using Equal Temperament. In key signatures with more accidentals, there will be more and more dissonant intervals. Historically, composers would often use these dissonances for effect. |
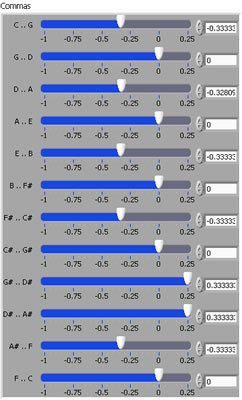 |
Download brochure (pdf)...