Music is based on sounds at different pitches, or frequencies. We usually make music with a relatively small set of pitches, each of which is called a note.

A temperament is a way of deciding just what the pitch will be for each note.

A bit of theory

We call the difference between two pitches an interval. Mathematically, the interval between two pitches is the ratio of their frequencies.
Some combinations of pitches sound better together than others.

For example, let’s take two pitches: the A above middle C, and the A just below middle C. The top A has a frequency of 440 Hz, and the lower A has a frequency of 220 Hz. The ratio between these two pitches is 440/220, which is mathematically equivalent to a ratio of 2/1. This interval is called an octave, and is found in almost all musical systems.
Our ears are remarkably sensitive to this interval. If we listen to an interval which is even slightly different from an octave, it sounds unnatural and out of tune to us.

Pure Intervals

In general, intervals where the frequencies are the ratio of two small numbers, sound better to our ears than intervals which aren’t. Some of the important intervals in Western music are:

1/2    = an octave
2/3    = a fifth
3/4    = a fourth
4/5    = a major third
5/6    = a minor third
3/5    = a major sixth
We call these pure intervals. Not only are these intervals the ratio of two small numbers, they are natural harmonics. This means that in most instruments, when you play a note, the natural harmonics of the note are also present in the sound to some degree (the exact degree to which each harmonic is present is part of what gives an instrument its own unique sound).

Incompatible Intervals

Ideally, we would like to define a reasonably small group of pitches which would let all of these intervals be used freely. Unfortunately, this goal is unattainable.

We can demonstrate this by playing a circle of fifths. Start with any note, and play the note which is exactly a major fifth above it. Keep going, doubling back an octave when you have to, until you get back to your starting note. After playing 12 major fifths, you will have played every note exactly once, and also defined every interval that exists in a diatonic scale.

But ... If you followed the instructions, and played every major fifth as a pure interval, you would have ended up being about a quarter of a semitone away from your starting pitch.

We can demonstrate the same thing with a bit of arithmetic. There are twelve consecutive fifths in a circle of fifths. The same interval is covered by seven consecutive octaves. Saying this in mathematical terms:

The interval between seven octaves and a circle of fifths is about 23% of a semitone, and is referred to as a Pythagorean comma. The object of a temperament is to hide this comma somewhere where it won't sound too obvious.

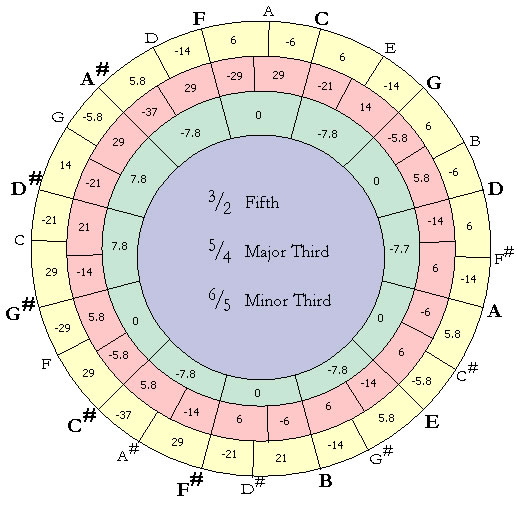
Here's what you see when you use Temperament Designer.

You see three circles:

1. Fifths
   The inner circle shows how much each of the major fifths are stretched or compressed. The numbers are in commas. Positive numbers mean that the interval has been stretched out: negative numbers mean that the fifth has been shrunk. If you add up all the numbers, you always get -1 (one comma).
2. Major thirds / Minor thirds
   You can think of a major fifth as being a major third, followed by a minor third (or the other way around).
   The outer two circles circle show the major and minor thirds inside each of the major fifths. Again, the numbers are the number of commas the intervals are away from being pure .
   

It's a lot of information in a very compact form!

Once you're worked out a temperament, you can try it out, and see how it sounds to you.

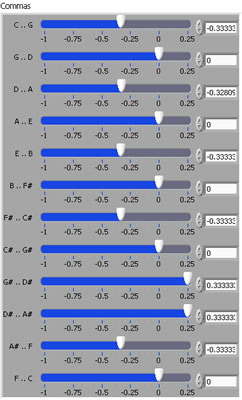
Traditionally, temperaments have been built by modifying the major fifths.

We make it easy for you by giving you sliders for each major fifth. The sliders automatically adjust to keep the overall adjustment (or comma) correct.

The units you are looking at is the comma. You can specify either the Pythagorean, or the Syntonic comma (which we haven't talked about yet).

The example we've been looking at is a historical temperament called Werkmeister IV. This is a temperament that give you almost pure major fifths and major thirds in key signatures with up to three sharps, or two flats. In many cases, music which these key signatures will sound startlingly clearer than if it is played using Equal Temperament.

In key signatures with more accidentals, there will be more and more dissonant intervals. Historically, composers would often use these dissonances for effect.